Heisenberg și simetriile lui Platon
Spre deosebire de oamenii de știință din vremea noastră, Werner Heisenberg avea conștiința dimensiunii culturale a fizicii, a locului ei în istoria spiritului și a fondului teoretic care a făcut-o posibilă. Pentru fizicianul german, marea antinomie care a străbătut istoria fizicii provine din confruntarea dintre Democrit și Platon. Filosoful din Abdera postulează indivizibilitatea elementelor ultime și explică ordinea lumii pornind de la polaritatea dintre plin și gol, pe când Platon descoperă „particulele elementare care sunt obiecte matematice fundamentale de o înaltă simetrie.”[1] Elementele fundamentale ale lumii pot fi descompuse în mici „corpuri” pe care, spune Platon „trebuie să le concepem atât de mici încât, luat unul câte unul, fiecare să fie, datorită micimii sale, invizibil pentru noi.” (Timaios, 56c)[2]. Aceste corpuri sunt structuri geometrice, reductibile la două tipuri de triunghiuri, iar „triunghiurile înseși nu sunt materie, sunt doar formă matematică”[3] Marea antinomie se referă numai în primă instanță la opoziția divizibil – indivizibil, analizată de Kant în Critica rațiunii pure. Ea trimite în fapt la relația dintre simetrie și materie. Este simetria fundament al materiei sau materia precede structurile simetrice? Heisenberg crede că mecanica cuantică a rezolvat pentru totdeauna această problemă în favoarea formei teoretice platoniciene, cea în care simetria precede și fundamentează existența materială. Heisenberg nu se întoarce la microfizica lui Platon din rațiuni pur istorice. El nu-și caută predecesori, ci dimpotrivă, crede că felul în care filosofii greci au pus problemele, precum și soluțiile lor, pot servi drept model pentru fizica nouă, fiindcă „înțelegerea teoriei cuantice poate fi adâncită prin studierea respectivelor formulări antice ale problemelor.”[4] De vreme ce fizica de la Planck încoace manifestă „o întoarcere de la Democrit la Platon”[5], trebuie să revenim la filosoful grec pentru a înțelege mai bine structura teoretică și metafizică în care se întemeiază teoria cuantică.
Heisenberg a avut de-a lungul întregii vieți un adevărat cult pentru dialogul platonician Timaios: de la perioada liceului clasic, când traducerea din greacă a pasajului despre cele mai mici părți ale materiei îl uimea, până în perioada târzie, când i se părea că poate identifica o structură platoniciană în ecuația lui Dirac. Ce a descoperit fizicianul german atât de spectaculos în acest dialog platonician? Spus foarte simplu: forma teoretică a teoriei finale a fizicii.
Timaios este un dialog care face parte din procesul de coborâre organizată de la nivelul formelor ideale la cel al realului concret. Prima parte a dialogului descrie structura universului la nivel macro și avansează o ipoteză revoluționară, care va deveni o achiziție perenă a astronomiei, anume că o mișcare neregulată poate fi explicată prin combinarea a două mișcări regulate distincte. Această construcție a priori a arhitecturii cinematice a universului este alcătuită din două mișcări fundamentale, cea a identicului, către dreapta, și cea a diferitului către stânga, în diagonală, a căror compunere dă încă șapte mișcări distincte. E important de subliniat că Platon descrie o structură cinematică pură, care precede existența astrelor, structurată matematic astfel încât să facă posibilă apariția corpurilor. Sufletul lumii, conținătorul acestor mișcări a priori, poate fi văzut ca prima formulare a noțiunii fizice de câmp. Acest suflet atotcuprinzător e un câmp de simetrii care conține două serii geometrice care fac posibilă apariția figurilor în spațiu.
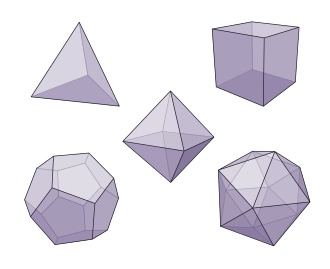
Această mișcare absolut ordonată e contrastată de zgâlțiala complet lipsită de ordine proprie lui χώρα, acea „realitate invizibilă și fără formă, atotprimitoare, participând într-un fel greu de înțeles la inteligibil” (Timaios 51b). Demiurgul întipărește simetriile a priori în această existență plasmatică, ce nu e nici spațiu, nici materie,: „toate acestea se aflau în dezordine, iar zeul a introdus simetrii în toate, atât în relație cu sine, cât și între ele (πρὸς αὑτὸ καὶ πρὸς ἄλληλα συμμετρίας ἐνεποίησεν) (Timaios 69 b). Înainte de a introduce simetriile de la nivel macro, Demiurgul se îndreaptă spre nivelul microfizic, unde va deduce în mod a priori cinci poliedre regulate exclusiv din determinarea pură a spațiului, poliedre care vor funcționa ca particule din compunerea cărora vor fi generate cele cinci elemente fundamentale ale lumii: apa, focul, aerul, pământul și eterul. Heisenberg descrie procedura platoniciană astfel: „particulele elementare din filosofia lui Platon își obțineau simetria din așa-numitul grup al spațiului, grupul rotațiilor în spațiul tridimesional.”[6] Cu alte cuvinte, cele cinci poliedre regulate convexe, tetraedrul, hexaedrul, octaedrul, dodecaedrul și icosaedrul, sunt singurele structuri care-și păstrează identitatea după epuizarea tuturor transformărilor rotaționale în spațiul tridimensional. Ele nu sunt propriu-zis corpuri, ci structuri invariante. Simetria lor este identitate în diferență, adică invarianță în transformare. Aceste structuri geometrice sunt deci rezultatul unei simetrii pur matematice a spațiului, una care dă seama de alcătuirea materiei și de posibilitatea transfomării elementelor unele în altele. Heisenberg crede că aceeași structură e activă în teoria cuantică: „Teoria finală a materiei va putea fi caracterizată, la fel ca și la Platon, printr-o serie de exigențe de simetrie importante, pe care astăzi le putem indica deja. Aceste simetrii nu mai pot fi explicate simplu prin figuri și imagini, așa cum fusese posibil pentru corpurile platoniciene, ci prin ecuații…Trebuie să considerăm ecuația materiei ca o expresie extrem de simplificată a exigențelor de simetrie. De aceea, ca și în cazul lui Platon, se pare că această lume de particule elementare și câmpuri de forță, aparent atât de complicată ar avea la bază o structură matematică simplă și transparentă.”[7] Cu alte cuvinte, deși exigențele de simetrie au devenit mult mai complexe decât cele platoniciene, raportul dintre simetrie și particulele elementare a rămas același. Simetria e cea care determină structura și existența particulelor și nu invers. Dacă adăugăm și analiza pe care Heisenberg o face ecuației lui Dirac, am putea trage concluzia că mecanica cuantică e o generalizare a microfizicii din Timaios. Unii cercetători au găsit acest model platonic nu numai în reflecțiile filosofice ale lui Heisenberg, ci și în articolele sale științifice. Un exemplu în acest sens este oferit de cercetarea recentă a lui Thomas Brückner, care afirmă, referindu-se la articolul lui Heisenberg din 1932 Űber den Bau der Atomkerne, că ideea unei particule originare numită Nucleon este rezultatul unei influențe a modelului platonician.[8]
Și totuși Heisenberg se oprește la jumătatea drumului. Simetria este rezultatul compunerii celor cinci genuri supreme din Sofistul. Ea poate fi deci descompusă, fiindcă platonician vorbind este identitate în diferență și mișcare în repaus. Ontologia lui Platon poate fi regândită de la această nouă formă a simetriei.
[1] Werner Heisenberg, Pași peste granițe, Editura Politică, București, 1977, traducere și studiu introductiv de Ilie Pârvu, p.16
[2] Platon, Opere VII, Editura Științifică, Bucuești, 1993, traducere de Cătălin Partenie
[3] Werner Heisenberg, Pași peste granițe, ed.cit, p.16
[4] Ibidem, p.23
[5] Ibidem, p.24
[6] Ibidem, p.33
[7] Ibidem, p.33-34
[8] Thomas Christian Brückner, Zur Ontologie der Elementarteilchen. Eine philosophische Analyse der aktuellen Elementarteilchenphysik, Springer Spektrum, 2015, p.25
INDICAȚII DE CITARE
Dragoș Grusea, „Heisenberg și simetriile lui Platon” în Anthropos. Revista de filosofie, arte și umanioare nr. 8-9/2025
Acest articol este protejat de legea drepturilor de autor; orice reproducere / preluare integrală sau parțială, fără indicarea sursei, este strict interzisă.


